Physics-informed dynamic mode decomposition (piDMD)
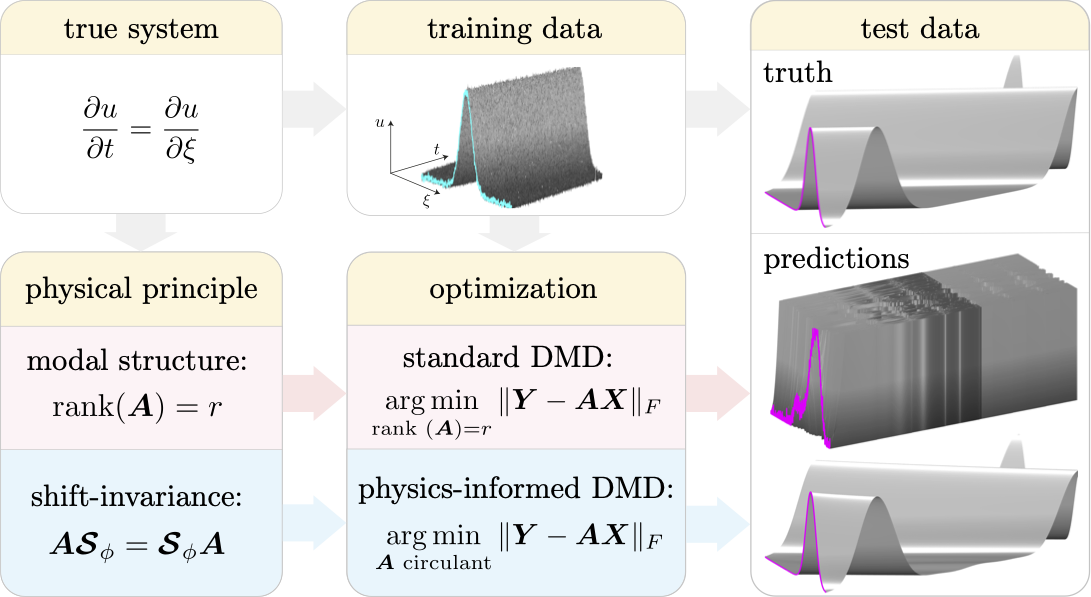
In this work, we demonstrate how physical principles -- such as symmetries, invariances, and conservation laws -- can be integrated into the dynamic mode decomposition (DMD). DMD is a widely-used data analysis technique that extracts low-rank modal structures and dynamics from high-dimensional measurements. However, DMD frequently produces models that are sensitive to noise, fail to generalize outside the training data, and violate basic physical laws. Our physics-informed DMD (piDMD) optimization, which may be formulated as a Procrustes problem, restricts the family of admissible models to a matrix manifold that respects the physical structure of the system. We focus on five fundamental physical principles -- conservation, self-adjointness, localization, causality, and shift-invariance -- and derive several closed-form solutions and efficient algorithms for the corresponding piDMD optimizations. With fewer degrees of freedom, piDMD models are less prone to overfitting, require less training data, and are often less computationally expensive to build than standard DMD models. We demonstrate piDMD on a range of challenging problems in the physical sciences, including energy-preserving fluid flow, travelling-wave systems, the Schr\"odinger equation, solute advection-diffusion, a system with causal dynamics, and three-dimensional transitional channel flow. In each case, piDMD significantly outperforms standard DMD in metrics such as spectral identification, state prediction, and estimation of optimal forcings and responses.
PDF Abstract