Multilevel domain decomposition-based architectures for physics-informed neural networks
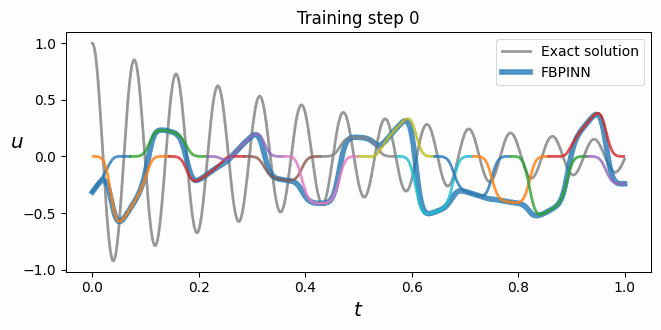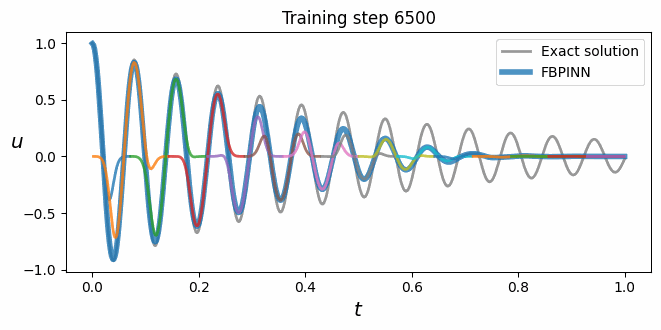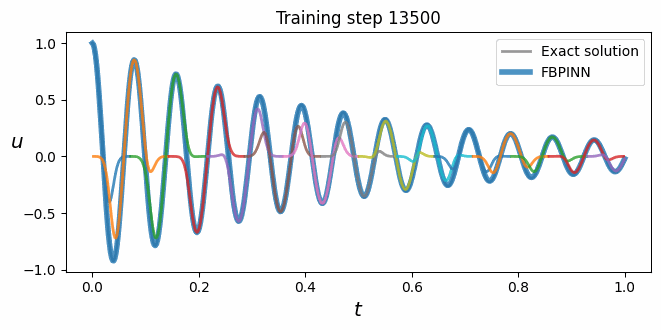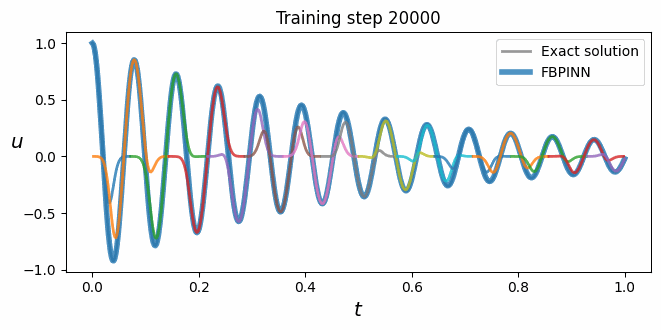
Physics-informed neural networks (PINNs) are a powerful approach for solving problems involving differential equations, yet they often struggle to solve problems with high frequency and/or multi-scale solutions. Finite basis physics-informed neural networks (FBPINNs) improve the performance of PINNs in this regime by combining them with an overlapping domain decomposition approach. In this work, FBPINNs are extended by adding multiple levels of domain decompositions to their solution ansatz, inspired by classical multilevel Schwarz domain decomposition methods (DDMs). Analogous to typical tests for classical DDMs, we assess how the accuracy of PINNs, FBPINNs and multilevel FBPINNs scale with respect to computational effort and solution complexity by carrying out strong and weak scaling tests. Our numerical results show that the proposed multilevel FBPINNs consistently and significantly outperform PINNs across a range of problems with high frequency and multi-scale solutions. Furthermore, as expected in classical DDMs, we show that multilevel FBPINNs improve the accuracy of FBPINNs when using large numbers of subdomains by aiding global communication between subdomains.
PDF Abstract