Global Optimization via Schr{ö}dinger-F{ö}llmer Diffusion
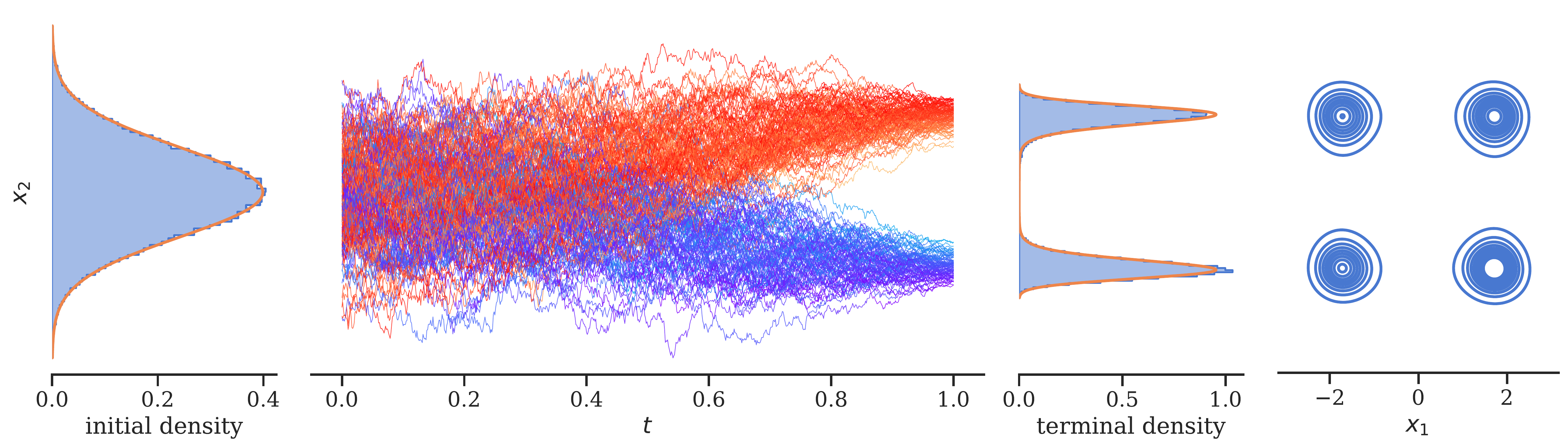
We study the problem of finding global minimizers of $V(x):\mathbb{R}^d\rightarrow\mathbb{R}$ approximately via sampling from a probability distribution $\mu_{\sigma}$ with density $p_{\sigma}(x)=\dfrac{\exp(-V(x)/\sigma)}{\int_{\mathbb R^d} \exp(-V(y)/\sigma) dy }$ with respect to the Lebesgue measure for $\sigma \in (0,1]$ small enough. We analyze a sampler based on the Euler-Maruyama discretization of the Schr{\"o}dinger-F{\"o}llmer diffusion processes with stochastic approximation under appropriate assumptions on the step size $s$ and the potential $V$. We prove that the output of the proposed sampler is an approximate global minimizer of $V(x)$ with high probability at cost of sampling $\mathcal{O}(d^{3})$ standard normal random variables. Numerical studies illustrate the effectiveness of the proposed method and its superiority to the Langevin method.
PDF Abstract