Network Design for Controllability Metrics
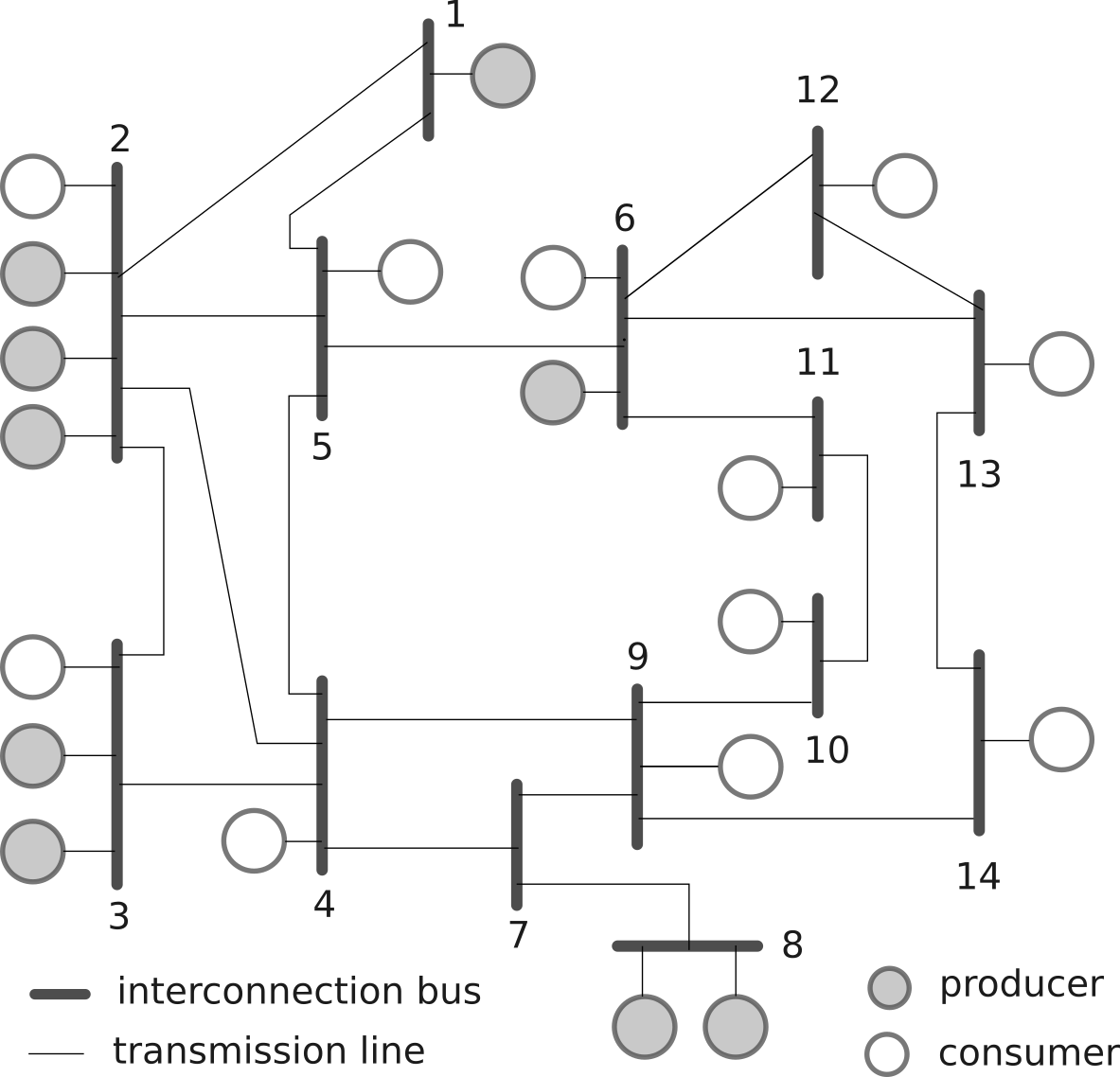
In this paper, we consider the problem of tuning the edge weights of a networked system described by linear time-invariant dynamics. We assume that the topology of the underlying network is fixed and that the set of feasible edge weights is a given polytope. In this setting, we first consider a feasibility problem consisting of tuning the edge weights such that certain controllability properties are satisfied. The particular controllability properties under consideration are (i) a lower bound on the smallest eigenvalue of the controllability Gramian, which is related to the worst-case energy needed to control the system, and (ii) an upper bound on the trace of the Gramian inverse, which is related to the average control energy. In both cases, the edge-tuning problem can be stated as a feasibility problem involving bilinear matrix equalities, which we approach using a sequence of convex relaxations. Furthermore, we also address a design problem consisting of finding edge weights able to satisfy the aforementioned controllability constraints while seeking to minimize a cost function of the edge weights, which we assume to be convex. In particular, we consider a sparsity-promoting cost function aiming to penalize the number of edges whose weights are modified. Finally, we verify our results with numerical simulations over many random network realizations as well as with an IEEE 14-bus power system topology.
PDF Abstract