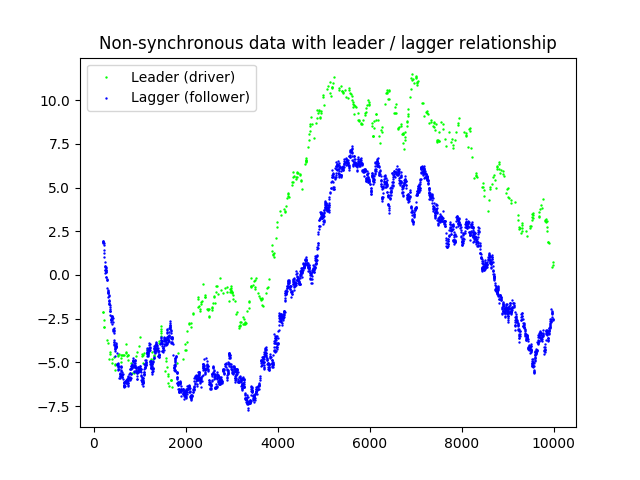
Estimation of the lead-lag parameter from non-synchronous data
We propose a simple continuous time model for modeling the lead-lag effect between two financial assets. A two-dimensional process $(X_t,Y_t)$ reproduces a lead-lag effect if, for some time shift $\vartheta\in \mathbb{R}$, the process $(X_t,Y_{t+\vartheta})$ is a semi-martingale with respect to a certain filtration. The value of the time shift $\vartheta$ is the lead-lag parameter. Depending on the underlying filtration, the standard no-arbitrage case is obtained for $\vartheta=0$. We study the problem of estimating the unknown parameter $\vartheta\in \mathbb{R}$, given randomly sampled non-synchronous data from $(X_t)$ and $(Y_t)$. By applying a certain contrast optimization based on a modified version of the Hayashi-Yoshida covariation estimator, we obtain a consistent estimator of the lead-lag parameter, together with an explicit rate of convergence governed by the sparsity of the sampling design.
PDF Abstract